Divide & Conquer Monte Carlo Tree Search For Goal Directed Planning

This is a explanatory piece on the paper titled Divide & Conquer Monte Carlo Tree Search For Goal Directed Planning by Parascandolo, Buesing, et.al.

Path planning! What's that?🙄

To put simply, path planning is the process of finding a suitable path from a starting configuration to some desired goal. Think of it as the process that you unconsiously make all the time when you need almost anything done. For example, you need to go to your school from your house. You unconsciously decide on a particular path that you take. You could, in theory take and infinite number of paths from your house to your school. But, you would settle for something that is more easy to execute. Maybe avoid going through the street where you know you could most probably bump into your ex! This whole process that you sometimes do not even think about is path planning in general.

Path planning in general involves exploring states from the starting state and making our way to the goal state. Or, in some cases, we might start from the goal state and explore possible states and reach our starting state. You might even have tried using the latter while solving mazes, where you start exploring the possiblities from the goal and try to make your way towards the state state.

So how do we path plan!? or plan a path! 🤔

Imagine you are trying to solve a maze and you can take any of the four actions - up, down, right and left, to move to the next state. At every state you can potentially take four actions each action leading to the next state. If you know what the next state will be given you perform a particular action at some state, you could potentially explore all the possible sequences of actions and then consider executing the one that suits you. However, by the time you would have calculated all these possibilites, you might have missed your school!!

At each state you have some number of actions that you can take, leading to another set of states, each of which would have almost the same set of possible actions, leading to an exponential growth of possibilites with respect to the length of actions considered. Going through each and every one of these possibilities isn't a good idea. Many path planning solutions deal with this exponential blow off my using certain assumptions and workarounds so that they do not have to consider all the possibilities.

Monte Carlo Tree Search (MCTS) 🌲

In this paper, the authors suggest an imporovement over the traditional Monte Calro Tree Search algorithm. I'll try to explain the main idea behind the Monte Carlo Tree Seach¹.

Monte Carlo Tree Seach works by building a tree wherein the root would represent the start state and the child node would represent the states you would end up in after performing an action. Each of these nodes also has a value attached with it depecting the value of being at that state. Initially we do not know about the value of a state and so we initialize it with $0$.

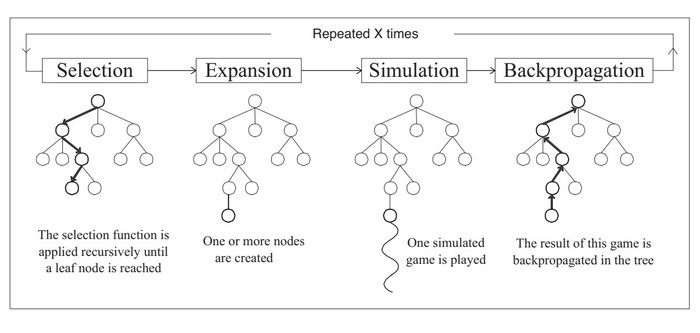Monte Carlo Tree Search Algorithm. Source: Chaslot(2006)

The search works by randomly selecting a node to explore and then performs a series of simulations to check how good is it to be at that state. The values of the current state and subsequent parents are recursively updated. Modern flavours of MCTS use do not explore the tree to only some depth and use a function approximator to store the values of the nodes. This is what Google's Aplha Go did to some extent! They also had a lot of other stuff going on in their work, but MCTS was the backbone of their method.

Okay!🥱 So what's so cool about this one!?

Imagine that you need to plan a euro trip with your friends and want to cover some of the known spots like the Eiffel Tower, the Colosseum, or the Big Ben. You could plan the whole trip yourself, which could take a while, or, you could delegate some of the tasks to your firends. And because you all have planned to visit the above places, one of you could plan the trip from the airport all the way to one of these spots, say the Eiffel tower. And the next person would plan the part from Eiffel to the Big Ben, and so on. This would save time as these planning task are being run in parallel. This is what the authors suggest in this paper.

“the order in which we construct a plan does not have to coincide with the order in which we execute it”.

So maybe we can break the planning process into smaller tasks which in turn are planning tasks themselves. This is the whole divide and conquer aspect of this paper which is very similar to the essence of dynammic programming!

The Details

The authors define a stochastic polciy $\pi = p(a|s, s_{\infty})$ which is a policy distribution over the actions given the current state $s$, the goal state $s_\infty$ and some embedding describing the environment². They also define a value of the policy $\pi$ as $v^\pi(s, s_\infty)$ which is basically the probability that we would end up in the goal state $s_\infty$ if we keep following the policy $\pi$. This policy is referred to as the goal-driven policy or the low level policy.

---

In the traditional Reinforcement Learning (RL) setting, the agent would try and move, performing a set of actions, gaining some experience from those actions and then learning a policy that would try and maximize the rewards. In planning however, we don't need to execute the actions. All we need to do is speculate the results of performing those actions. By doing this we can contemplate about the consequences of performing different sequences of actions, and thereby take the best possible action.

Further Reading

1. Divide & Conquer Monte Carlo Tree Search For Goal Directed Planning, Parascandolo, Buesing, et.al.
2. Monte-Carlo Tree Search: A New Framework for Game AI, Chaslot et al.
3. A Survey of Monte Carlo Tree Search Methods, Browne et al.
4. Mastering the game of Go with deep neural networks and tree search, Silver et al.